值迭代的采样复杂度
Published:
推导强化学习中值迭代的采样复杂度。
整理自 Chi Jin’s RL course, vidoe 6. 考虑一个用五元组($\mathcal{S}$, $\mathcal{A}$, r, $\mathbb{P}$, H) 刻画的马尔可夫决策过程 (MDP,Markov Decision Process). 其中, $\mathcal{S}$ 表示状态空间, $\mathcal{A}$ 表示动作空间,$r$ 表示回报函数,$\mathbb{P}$ 表示概率转移kernel,而 $H$ 表示horizon的大小。我们考虑模拟器存在下的离线强化学习场景,如下图所示。
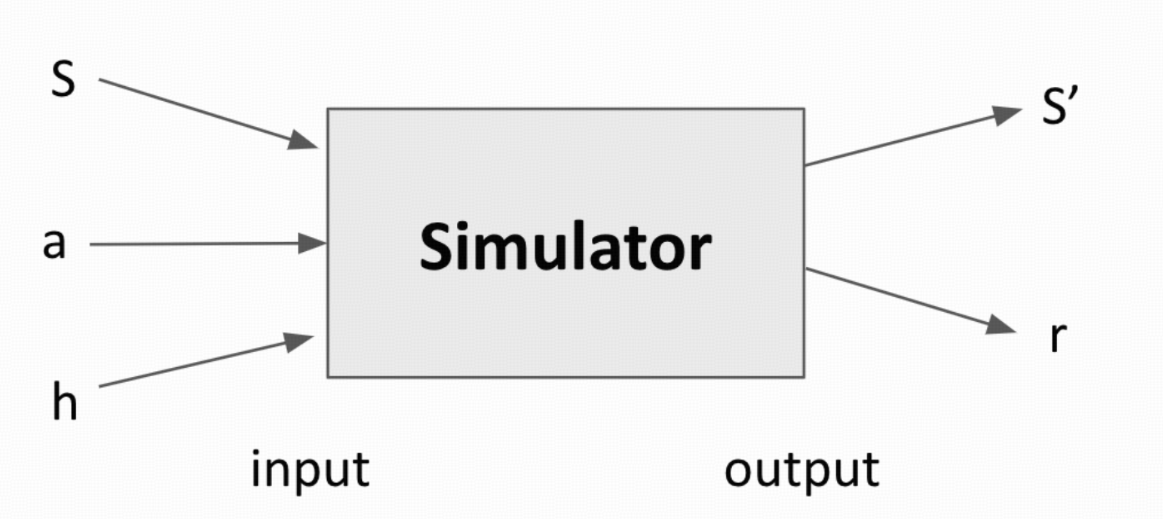
模拟器对于给定的输入 $(s,a,h)$,会输出 $s’ \sim \mathbb{P}(\,\cdot\, \mid s,a)$ 以及 $r = r_h(s,a)$. 在笔者早期 强化学习初步 博客中就已经介绍过值迭代算法,但是当时的算法假设已知 $\mathbb{P}$ 的设定,本篇文章主要介绍当 $\mathbb{P}$ 未知的时候的值迭代算法,如下:

算法的设计也十分直接:首先对于每一个元组 $(s,a,h)$ 独立的采样 $n$ 个样本然后用经验均值估计 $\hat{\mathbb{P}}_h(s’ \mid s,a)$ 估计真实转移概率 $\mathbb{P}_h(s’ \mid s,a)$. 然后用估计得到的模型利用Bellman方程运行值迭代算法。不难发现,当 $n$ 趋于无穷的时候上述算法应当和值迭代算法具有相同的保证,但是本文关注的核心问题是,值迭代算法的采样效率是多少,多大的 $n$ 可以保证得到一个 $\epsilon$ 解。回答该问题需要对上述过程进行很精细的分析,稍有不甚可能就会得到一个不紧的上界估计。 下面,我们会使用两个引理,推出最后关于算法采样复杂度的主要定理。
Lemma 1
我们叙述第一个引理:对于任意给定的元组 $(s,a,h) \in \mathcal{S} \times \mathcal{A} \times [H]$ 以及任意给定或者与 $\hat{\mathbb{P}}(\,\cdot\,\mid s,a)$ 独立的随机函数 $V \in [0,H]^S$, 以概率 $1-\delta$ 成立着
\[\begin{align*} \left \vert ( \hat{\mathbb{P}}_h - \mathbb{P}_h ) V(s,a) \right \vert \lesssim H \sqrt{ \log (HSA/ \delta ) /n }. \end{align*}\]该引理等价于分析如下量的集中性质:
\[\begin{align*} Z = \sum_{s' \in \mathcal{S}} (\hat{\mathbb{P}} (s' \mid s,a) - \mathbb{P}(s' \mid s,a )) V(s') \end{align*}\]上述量是 $s’ \in \mathcal{S}$ 以及 $i \in [n]$ 的求和. 根据Hoeffding集中不等式可以简单看出 $Z$ 的量级不会超过 $\sqrt{S /n}$, 但我们需要一个更紧的上界,原因是关于 $s’$ 上述估计量具有稀疏性。我们可以考虑交换求和顺序, 得到 $Z = \frac{1}{n} \sum_{i \in [n]} Y_i$, 其中
\[\begin{align*} Y_i &= \sum_{s' \in \mathcal{S}} (\mathbb{I}[s_i' = s'] - \mathbb{P}(s' \mid s,a)) V(s') \\ &= (1- \mathbb{P}(s_i' \mid s,a)) V(s_i') - \sum_{s' \ne s_i'} \mathbb{P}(s' \mid s,a) V(s') \end{align*}\]取范数后,我们有
\[\begin{align*} \vert Y_i \vert \le (1- \mathbb{P}(s_i' \mid s,a)) H + \sum_{s' \ne s_i'} \mathbb{P}(s' \mid s,a) H \le 2 H. \end{align*}\]那么,对于$Z = \frac{1}{n} \sum_{i \in [n]} Y_i$ 使用 Hoeffding集中不等式,我们就可以得到以概率 $1-\delta$ 成立着
\[\begin{align*} \vert Z \vert \le H \sqrt{\log (1/\delta)/n}. \end{align*}\]最终对所有的 $(s,a,h)$ 取联合界就可以得到我们想要证明的Lemma 1.
Lemma 2
我们叙述并且证明第二个引理,该引理严谨刻画了当 $\hat{\mathbb{P}}$ 与 $\mathbb{P}$ 很接近的时候,估计出来的值函数也会很接近。注意到
\[\begin{align*} &\quad V_h^\pi(s) - \hat V_h^\pi(s) \\ &= \mathbb{E}_\pi [Q_h^\pi (s,a) - \hat Q_h^\pi(s,a) \mid s_h = s] \\ &= \mathbb{E}_\pi [( \mathbb{P}_h V_{h+1}^\pi)(s,a) - (\hat{\mathbb{P}}_h \hat V_{h+1}^\pi)(s,a) \mid s_h = s] \\ &= \mathbb{E}_\pi [(( \mathbb{P}_h - {\hat{\mathbb{P}}_h} ) V_{h+1}^\pi)(s,a) + ( {\hat{\mathbb{P}}_h} ( V_{h+1}^\pi - \hat V_{h+1}^\pi ) )(s,a) \mid s_h = s ] \\ &= \mathbb{E}_\pi [(( \mathbb{P}_h - {\hat{\mathbb{P}}_h} ) V_{h+1}^\pi)(s,a) \mid s_h = s] + \mathbb{E}_{\hat M, \pi}[( {\hat{\mathbb{P}}_h} ( V_{h+1}^\pi - \hat V_{h+1}^\pi) )(s,a) \mid s_h = s ] , \end{align*}\]其中 $\hat M$ 表示以转移概率核函数 $\hat{\mathbb{P}}$ 所刻画的马尔可夫决策过程。展开上述的递推式,就得到了我们想要证明的第二个引理:
\[\begin{align*} V_h^\pi(s) - \hat V_h^\pi(s) = \mathbb{E}_{\hat M,\pi} \left[ \sum_{i=h}^H (( \mathbb{P}_i - \hat{\mathbb{P}}_i ) V_{i+1}^\pi) )(s_i,a_i) \mid s_h = s \right]. \end{align*}\]Theorem 1
结合上述两个引理,我们得到算法的采样复杂度保证。我们定义 $\hat \pi$ 为 MDP $\hat M$ 从状态 $s$ 开始所对应的最优策略,我们有
\[\begin{align*} &\quad V_1^{\pi^\ast}(s) - V_1^{\hat \pi}(s) \\ &= V_1^{\pi^\ast}(s) - \hat V_1^{\pi^\ast}(s) + \hat V_1^{\pi^\ast}(s) - V_1^{\hat \pi}(s) \\ &\le V_1^{\pi^\ast}(s) - \hat V_1^{\pi^\ast}(s) + \hat V_1^{\hat \pi}(s) - V_1^{\hat \pi}(s) \\ &= \mathbb{E}_{\hat M, \pi^\ast} \left[ \sum_{h=1}^H (( \mathbb{P}_h - \hat{\mathbb{P}}_h ) V_{h+1}^{\pi^\ast}) )(s_h,a_h) \mid s_1 = s \right] \\ &\quad - \mathbb{E}_{M, \hat \pi} \left[ \sum_{h=1}^H (( \mathbb{P}_h - \hat{\mathbb{P}}_h ) V_{h+1}^{\hat \pi}) )(s_h,a_h) \mid s_1 = s \right] \end{align*}\]根据上式,我们希望对求和项 $h \in [H]$ 中的每一项都使用Lemma 1,但值得注意的是我们需要仔细地检查Lemma 1的独立性假设,首先由于 $\pi^{\ast}$ 是一个固定的策略,我们知道 $\mathbb{P}_i - \hat{\mathbb{P}}_i$ 与 $V_{i+1}^{\pi^\ast}$ 是独立的,对于等式的最后一项,我们需要更为小心,因为 $V^{\hat \pi}$ 与 $\hat{\mathbb{P}}$是相关的。但实际上,由于 $V_{h+1}^{\hat \pi}$ 仅仅依赖于后续的策略 ${\hat \pi}_{h+1}, \hat \pi_{h+2},\cdots, \hat \pi_H$,而这些策略的选择又仅仅依赖于 $\hat{\mathbb{P}}_{h+1},\hat{\mathbb{P}}_{h+2}, \cdots, \hat{\mathbb{P}}_{H}$, 我们可以发现 $\mathbb{P}_h - \hat{\mathbb{P}}_h$ 与 $V_{h+1}^{\hat \pi}$ 也应该是独立的,因此Lemma 1仍然可以使用。使用后,我们可以得到以概率 $1-\delta$ 成立着
\[\begin{align*} V_1^{\pi^\ast}(s) - V_1^{\hat \pi}(s) \lesssim H^2 \sqrt{ \log (HSA/ \delta ) /n }. \end{align*}\]上式说明,为了得到一个 $\epsilon$解,也即使得上式右端项小于 $\epsilon$, 需要选择 $n = \tilde{\Omega} ( H^4 \epsilon^{-2} )$. 选择 $n$ 正好是这个量级的大小,并且注意到算法需要对所有的 $(s,a,h)$ 元组都采样 $n$ 次,最终的样本复杂度为 $\tilde{\mathcal{O}}(H^5 S A \epsilon^{-2})$.
