多臂老虎机的遗憾下界
Published:
多臂老虎机的遗憾下界推导。
本期内容整理自 Chi Jin’s RL course, vidoe 10-11. 在 多臂老虎机 一文中,我们介绍了多臂老虎机的几个经典算法,包括ETC算法、$\epsilon$-贪婪算法以及UCB算法。其中ETC算法和$\epsilon$-贪婪算法可以达到 $\tilde{\mathcal{O}}(A^{1/3} T^{2/3})$ 的遗憾界,而UCB算法可以达到更好的 $\tilde{\mathcal{O}}(\sqrt{AT})$ 的遗憾界。
本文我们证明UCB算法的最优性,我们将给出任意算法的复杂度下界,证明其当 $T > A$ 时都至少为$\Omega(\sqrt{AT})$.
我们定义随机算法为一个算法分布,当给定一个随机种子后变为确定性算法,并且考虑对于任意随机算法的遗憾下界,这定义为一个最困难的问题 $p$ 对于任意给定的随机算法 $\mathcal{A}$ 产生的最小遗憾,也即 $\sup_{p} \inf_{\mathcal{A}} \mathbb{E}[ {\rm Regret}_T(p,\mathcal{A})]$, 其中期望来自于算法本身的随机性以及交互过程中的随机性。根据著名的Yao’s 极小极大原则,事实上我们可以考虑给出一个问题的困难分布 $\mathcal{D}$,然后考虑随机从分布 $\mathcal{D}$ 中抽取问题后的期望遗憾界,并且由于最优的随机算法必然在某个随机种子取到,在推导的下界过程中实际上也可以假设算法是一个确定性算法 $\mathcal{A}_{\rm det}$。用数学语言,我们有
\[\begin{align*} \sup_{p} \inf_{\mathcal{A}} \mathbb{E}[ {\rm Regret}_T(p,\mathcal{A})] \ge \sup_{\mathcal{D}} \inf_{\mathcal{A}_{\rm det}} \mathbb{E}_{p \sim \mathcal{D}} [{\rm Regret}_T(p,\mathcal{A}_{\rm det})]. \end{align*}\]我们构造困难问题分布 $\mathcal{D}$ 为一类多臂老虎机,首先从 $[A]$ 中均匀采样臂 $a \in [A]$, 然后令每个臂的奖励都服从伯努利分布,其中臂 $a$ 奖励返回1的概率为 $1/2+ \epsilon$, 而其余的臂奖励返回0/1的概率都为 $1/2$. 简单用图示意如下:
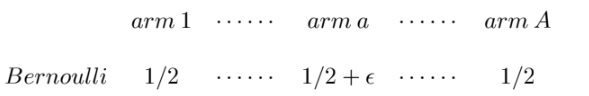
定义 $n_a$ 为臂 $a$ 被拉的次数,经过简单的计算我们可以知道
\[\begin{align*} \mathbb{E}_{\mathcal{D}} [{\rm Regret}(T)] = \epsilon \left[ T - \frac{1}{A} \sum_{a \in [A]} \mathbb{E}_a[n_a] \right]. \end{align*}\]下面我们重点关注 $\mathbb{E}_a[n_a]$ 的计算,为此我们考虑定义一个基准多臂老虎机,我们记 $\mathbb{E}_0[n_a]$ 为一个所有臂的奖励都服从参数参数为 $1/2$的伯努利分布的期望值。并且记 $R_{1:T}$ 为所有(可能的)奖励的轨迹,以及 $P_a$ 以及 $P_0$ 分别为困难多臂老虎机以及基准多臂老虎机关于 $R_{1:T}$ 的分布,那么我们有
\[\begin{align*} &\quad \mathbb{E}_a[n_a] - \mathbb{E}_0[n_a] \\ &= \sum_{R_{1:T}} n_a(R_{1:T}) [P_a(R_{1:T}) - P_0(R_{1:T}) ] \\ &\le T \sum_{R_{1:T}} \vert P_a(R_{1:T}) - P_0(R_{1:T}) \vert \\ &\le T \Vert P_a - P_0 \Vert_{\rm TV} \\ &\le T \sqrt{\frac{1}{2}{\rm KL}(P_0 \Vert P_a )}, \end{align*}\]最后一步使用了 Pinsker 不等式。 下面我们接着计算上面中与基准分布的KL散度
\[\begin{align*} &\quad {\rm KL}(P_0 \Vert P_a ) \\ &= \sum_{R_{1:T}} P_0(R_{1:T}) \log \frac{P_0(R_{1:T})}{P_a(R_{1:T})} \\ &= \sum_{t=1}^T \sum_{R_{1:T}}P_0(R_{1:T}) \log \frac{P_0(R_t \mid R_{1:t-1})}{P_a(R_t \mid R_{1:t-1})} \\ &= \sum_{t=1}^T \sum_{R_{1:t}} P_0(R_{1:T}) \log \frac{P_0(R_t \mid R_{1:t-1})}{P_a(R_t \mid R_{1:t-1})} \\ &= \sum_{t=1}^T \sum_{R_{1:t}: a_t(R_{1:t})=a} P_0(R_{1:T}) \log \frac{P_0(R_t \mid R_{1:t-1})}{P_a(R_t \mid R_{1:t-1})} \\ &= \sum_{t=1}^T \sum_{R_{1:t}: a_t(R_{1:t})=a} P_0(R_{1:T}) \frac{1}{2} \log \frac{1}{1- 4\epsilon^2} \\ &= \frac{1}{2} \mathbb{E}_0[n_a] \log \frac{1}{1- 4\epsilon^2}. \end{align*}\]由于基准多臂老虎机中每个臂的奖励分布完全一致,我们知道 $\sum_{a \in [A]} \mathbb{E}_0[n_a] = T$. 因此,回代入我们已经推导出关于遗憾下界的公式,我们知道
\[\begin{align*} &\quad \mathbb{E}_{\mathcal{D}} [{\rm Regret}(T)] \\ &= \epsilon \left[ T - \frac{T}{A} \sum_{a \in [A]} \mathbb{E}_a[n_a] \right] \\ &\ge \epsilon \left[T \left(1 - \frac{1}{A} \right) -\frac{T}{A} \sum_{a \in [A]} \sqrt{\frac{1}{2} {\rm KL}(P_0 \Vert P_a)} \right] \\ &= \epsilon \left[T \left(1 - \frac{1}{A} \right) -\frac{T}{2A} \sum_{a \in [A]} \sqrt{ \mathbb{E}_0[n_a] \log \frac{1}{1-4 \epsilon^2}} \right] \\ &\ge \epsilon \left[T \left(1 - \frac{1}{A} \right) -\frac{T}{2A} \sqrt{ AT \log \frac{1}{1-4 \epsilon^2}} \right] \\ &\ge \epsilon \left[T \left(1 - \frac{1}{A} \right) -\frac{T}{A} \sqrt{ \frac{AT \epsilon^2}{1-4 \epsilon^2}} \right] \end{align*}\]注意到上式的右端项为关于 $\epsilon$ 的二次函数,在 $T > A$ 的前提下我们选取 $\epsilon =\Theta(\sqrt{A/ T})$ 可以极大化右端项,最终得到遗憾下界至少为 $\Omega(\sqrt{AT})$.
注意到该遗憾下界可以被UCB算法达到,这就证明了UCB算法的最优性。
