图的动态连通性问题

图的动态连通性问题。笔者对相关论文的数据结构和算法进行整理，但是只能窥得作者的妙思的一二，很多精髓仍未掌握。但将整理的内容配图放在这里，希望一来加深自己的理解，二来希望对后续读到相关工作的人有所帮助。

Preliminaries

我们关注图上的动态连通性问题，图中可以会有结点和边的变动，我们希望动态地维护所有结点的连通性信息。

算法的基础是动态数结构，经典得例子包括Link-Cut Tree 或者欧拉回路树，这两种数据结构都可以在摊还意义下 $O(\log n)$ 的时间内支持三种操作，Link，Cut，以及Find-Root。也即将两棵树合并，分开，或者返回其树根，从而用来判断是否连通。

因此，这样就可以实现树上的动态连通性问题。

出于文章的完整性，我们对欧拉回路树进行简要的介绍。首先，树是没有欧拉回路的，但我们可以如下将一棵树的每条无向边变为两条有向边，然后再这样定义出的图上定义欧拉回路。

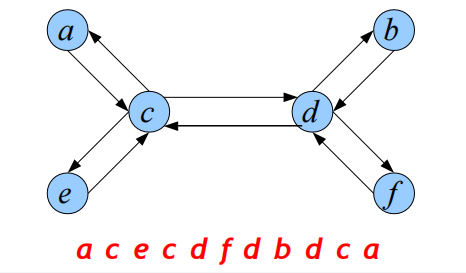
借助欧拉回路我们可以简单地实现Link-Cut操作，比如对于Link操作，考虑如下两棵树以及对应的欧拉回路，我们希望沿着黄色的节点进行Link操作，

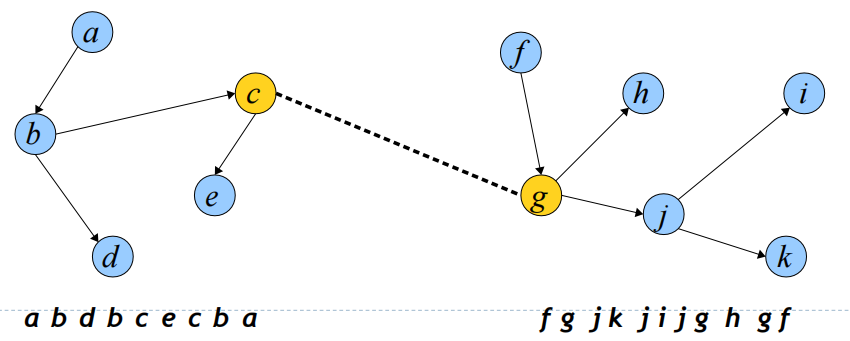
我们首先将两棵树的欧拉回路沿着要进行Link操作的结点进行旋转，得到

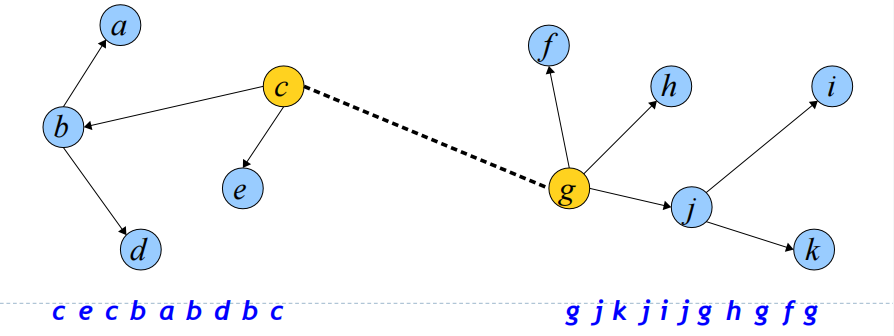
然后就可以直接进行Link操作得到合并后的树

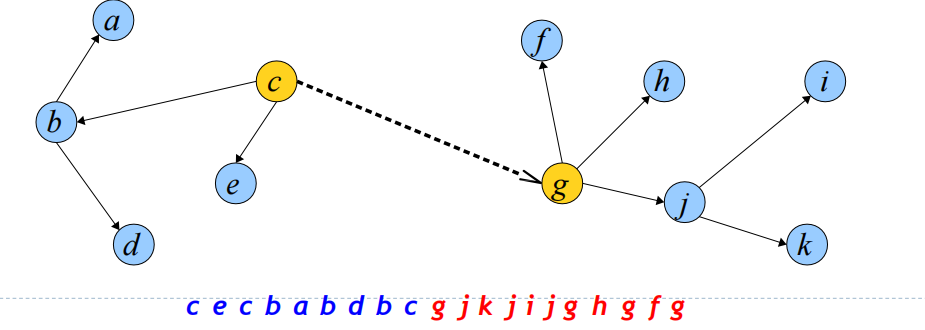
类似的，我们也可以简单地执行Cut操作，以下面为例

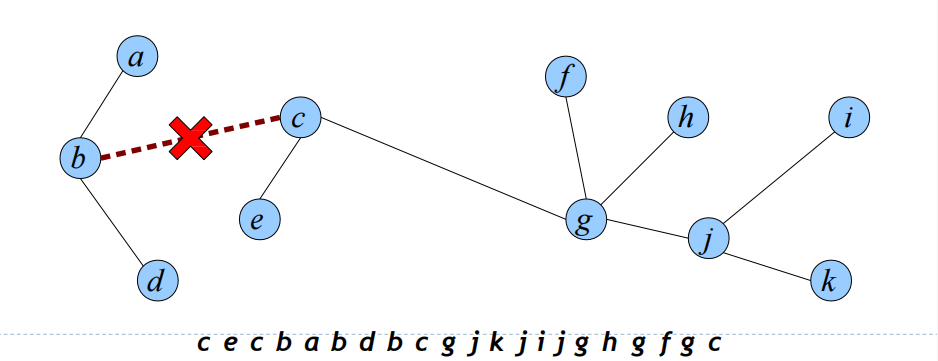
进行切断操作后会得到三段欧拉回路

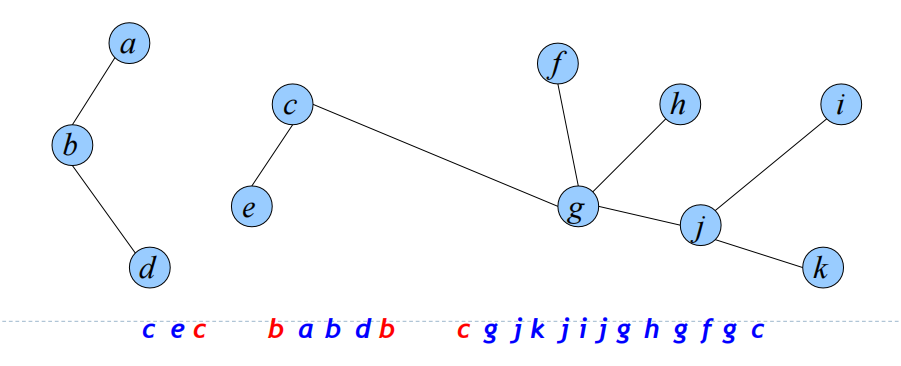
我们进行重组后就可以得到切断后的欧拉回路如下，

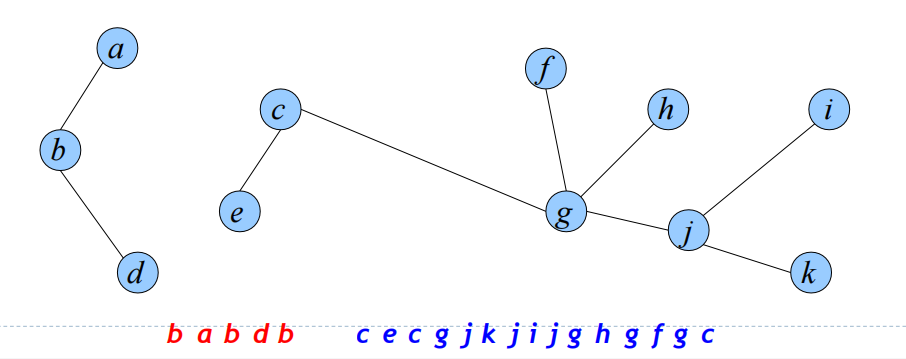
根据上面的描述，Link/Cut操作只需要 $O(1)$ 的时间，但每次需要进行区间的拆分/合并等操作，我们通过Splay Tree维护该操作，Splay Tree是一个自平衡的二叉查找树，由于二叉查找树中的一棵子树对应于一个区间，并且Splay Tree上的区间拆分/合并等操作都只需要 $O(\log n)$ 的时间，最终使用Splay Tree实现的欧拉回路树仅需要 $O(\log n)$ 的时间。

Dynamic Edge Connectivity

根据上一小节，我们知道树上的动态连通性问题非常好解决。但我们关注与图上的动态连通性问题，我们将从树上的连通性出发，设计解决图上的动态连通性的数据结构和算法。我们的想法是动态地维护一个生成森林，借此来回答连通性问题，如下图所示

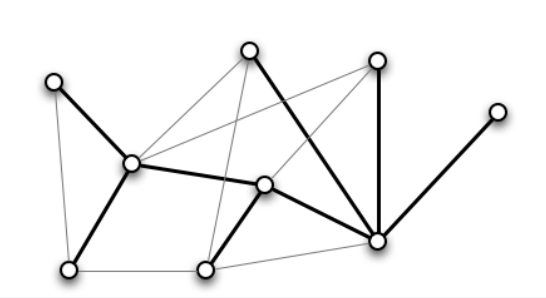
与树上的连通性问题不同，此时在删除一条边的时候，并不意味着两个部分不连通

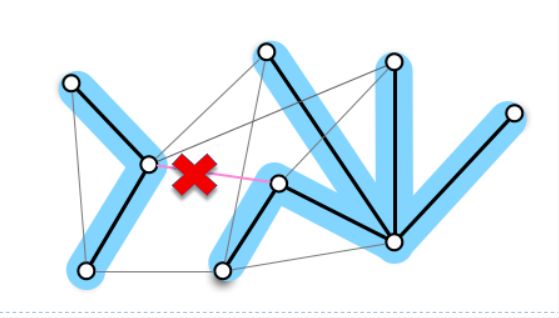
如上面这个例子，删除一条粉色的边，使得蓝色的两棵树互不连通，但是在图上他们仍然是连通的，我们需要寻找到一条置换边，置换掉被删除的边，如下图所示：

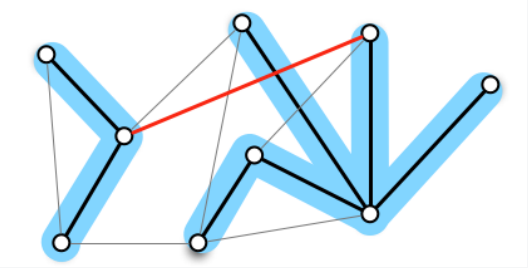
问题的难点在于我们不希望暴力地枚举所有边，而希望一种聪明的算法，尽可能快速地找到像这样的置换边。

我们将介绍 STOC 1998 文章 “Poly-Logarithmic Deterministic Fully-Dynamic Graph Algorithms” 中所给出的算法。

对于一个图，我们建立一个分层图，其中包含 $O(\log n)$ 层，第 $i$ 层 结点数目不超过 $n / 2^i$.每层维护一些边集合，构成一张图，并且记录图上的一个随机森林，保证下层的森林严格包含上层的森林，并且最下层是原图的生成树，而且如果一条边在某一层是树边，在其下的所有层它也都将是树边，如下所示：

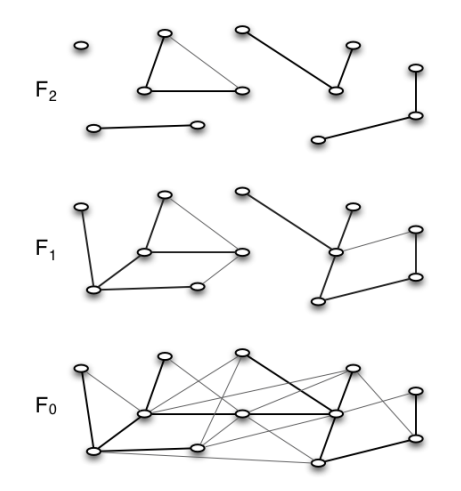
添边时我们从下面最后一层添加，如果新增的边合并了两棵树，将其变成树边，反之设置为非树边。

删边的时候，如果删除的边将树分成两个部分，我们需要寻找到一个置换边，将树重新连接起来。

我们自顶向下寻找置换边，如果在第i层寻找到了某条置换边，那么我们将其插入i层下面的所有层作为置换边，就不用往下面搜索了如果搜寻不到置换边，我们进入下一层继续搜索，在第i层时，我们知道此时的树被分割成两部分，其中较小的部分至多只有 $n / 2^{i+1}$ 个结点，因此我们将该部分复制一份到上一层中，然后我们依次考虑较小的树的所有邻接的边，如果其连接了两个树，我们就找到了一条置换边，如果其没有连接两棵树，那么它一定被包含在原来的树内，我们可以将这条边挪到上一层中。

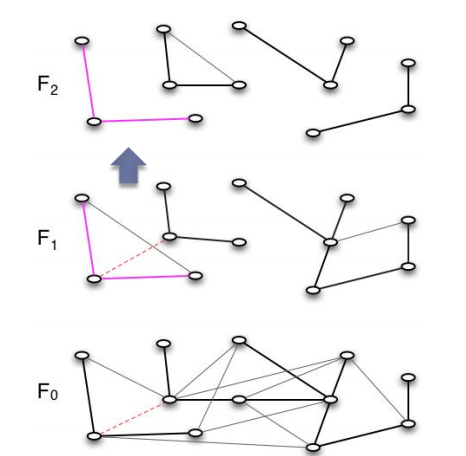
我们来看下面这个运行的例子，考虑在该分层图中以如下的方式删除一条边，

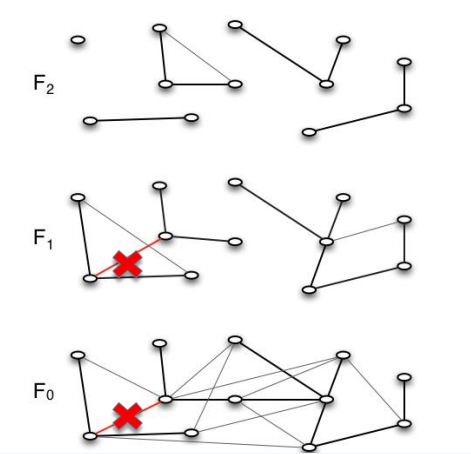
这条边同时处于第0层和第1层，我们在第1层开始搜索置换边，首先第1层原来该边所连接的树被分成了两个部分，我们将较小的部分，也就是下图中所示的粉色的部分，复制一份到上一层中。

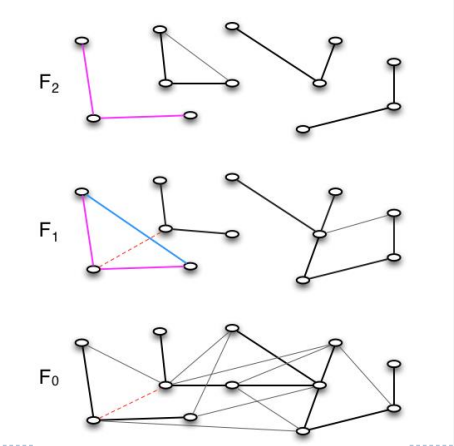
我们在第1层中考虑粉色部分邻近的所有边，我们发现下图所示的蓝色的边，不为置换边，所以其一定在粉色的部分内，我们可以将蓝色的边整条边都挪到上一层中，

挪动之后的结果如下图所示

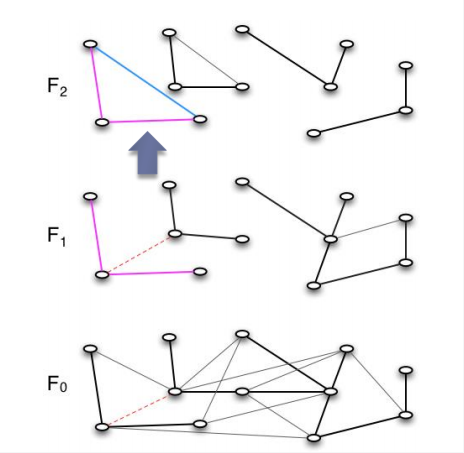
至此，我们已经在第1层的粉色部分中考虑了所有邻接的边，但是未能找到任何一条置换边，因此我们进入下一层继续搜索，最后我们找到了第1层的如下所示蓝色的边，可以重新连接，

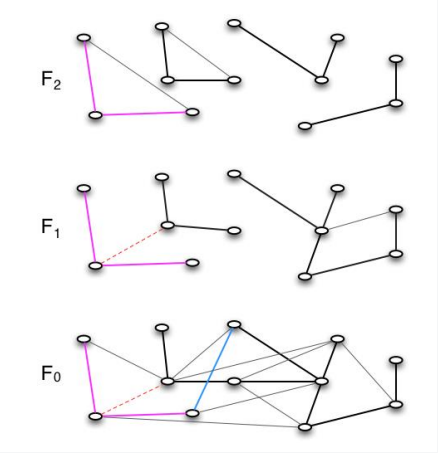
可以验证，上述的流程可以始终使得分层图保持其原来的性质。

下面我们简要分析算法的复杂度，首先我们采用欧拉回路树作为数据结构，Link / Cut 以及判断连通性等操作都可以在 $O(\log n)$ 摊还时间内完成，分析算法每个操作的复杂度，可以发现整体的代价为 $O(\log^2 n)$. 下面以最复杂的删边操作为例子，每一层删除的直接代价为 $O(\log n)$， 最坏情况下需要在所有层都删除，代价为 $O(\log^2 n)$. 删边后我们需要递归地寻找置换边，有可能导致复杂度变高的时候在于一直找不到置换边所以一直递归进行，但注意到这样的失败的总次数并不可能太多，这是因此每次失败都会将该边一次性地的层数增加。增加每条边都需要 $O(\log n)$ 的代价，但由于层数至多只有 $O(\log n)$ 层，每条边的层数的增加次数至多也只有这么多次，那么总体意义下该操作的摊还时间也为 $O(\log^2 n)$. 最终我们找到一条置换边，我们在第i层以及该层以下的所有层都将其设为新的树边，整体的代价为 $O(\log^2 n)$.

注意到上述的分析实际上省略了很多细节，包括如何使用欧拉回路树来实现整个算法流程中的所有操作。上述分析只为了大致展示其复杂度的来源，更详细的分析请参考原文。

Decremental Minimal Spanning Tree

上述的算法进行简单地改动，可以使得其可以支持decremental地最小生成树问题，其中decremental指的是动态图中只有删边操作，没有加边操作，当然存在一种归约可以用decremental的最小生成树问题来解决fully dynamic的最小生成树问题，其中fully dynamic 也即既支持删边操作又支持加边操作。

算法的改动很小，只需要在考虑所有邻接边的时候，以边的权重从小到大的顺序依次进行考虑即可，难点在于证明这样的算法确实动态地维护了一个最小生成树。我们想要证明，所描述的算法流程总会维持下面这个不变式：如果 $e$ 是一个环 $C$ 中权重最大的边，那么他在 $C$ 的所有边中的层数一定是最低的。

我们首先看为什么该不变式蕴含着算法的正确性。我们下面证明，这个不变式意味着对于任何的树边 $e$，其任何置换边中权重最小的一条边总是在最高层。因此我们的算法自顶向下搜寻置换边的流程可以保证动态地维护最小生成树。

我们配合着如下的例子证明上述论断，对于树边 $e$ , 我们考虑其两条置换边 $e_1,e_2$, 在下图中用蓝色的边表示，其权值分别为3 和 6

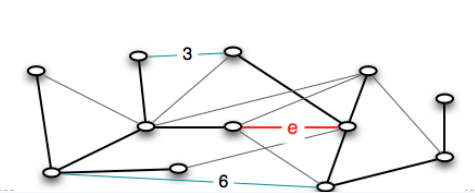
这样这两条置换边可以构成两个环 $C_1,C_2$, 如下图所示。且我们知道在 $C_1,C_2$ 中置换边 $e_1,e_2$ 一定都是各自的环中最大的拿一条边，否则原来的树结构不为最小生成树，

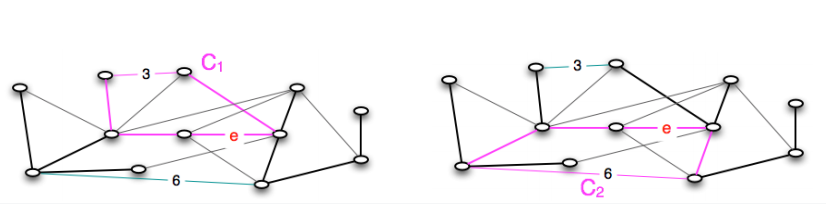
这样一来，考虑如下构成的环，假设 $e_1>e_2$ 那么我们知道 $e_1$ 一定是该环中最大的一条边，根据我们的不变式， $e_1$ 一定具有该环中最低的层数，其层数自然就低于$e_2$。 反过来说，权重最小的置换边一定位于最低层，因此我们可以自顶向下进行搜索。

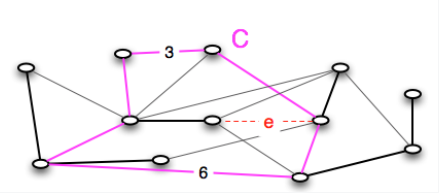
下面我们证明算法一直维护着上述的不变式。

假设 $e$ 是一个环 $C$ 中权重最大的边，将其删除并不会违背这个不变式，有可能违背这个不变式的情况在于其层数增加的时候。

首先树边不可能是环中权重最大的边，不然会违背我们正在维护最小生成树的性质。因此 $e$ 一定是非树边，当其从 第 $i$ 层被移动到第 $i+1$ 层的时候，它一定是第 $i$ 层里面邻接着我们想要连接的树 $T_v$ 中权重最小的边。根据我们的不变式，环 $C$ 中所有的边的层数至少都为 $i$. 我们又知道我们再考虑第i层的时候我们总是优先考虑权重小的边，而 $e$ 在环 $C$ 中权重最大，那么环 $C$ 中所有的与 $T_v$ 邻接的所有边的层数都至少为 $i+1$. 但实际上，环 $C$ 中所有的边都应该与 $T_v$ 邻接。 否则的话，环 $C$ 可以离开 $T_v$, 那么一定存在一条边 $f \ne e$, $f$ 说一条置换边，但是环 $C$ 中所有的与 $T_v$ 邻接的所有边的层数都至少为 $i+1$， 可是算法在第 i层寻找置换边的前提是第$i+1$ 层都找不到任何置换边了，矛盾。所以环 $C$ 中所有的边都应该与 $T_v$ 邻接， 而我们又已经推导出 环 $C$ 中所有的与 $T_v$ 邻接的所有边的层数都至少为 $i+1$。 这意味着环 $C$ 中所有的边的层数都至少为 $i+1$, 因此将边 $e$ 的层数增高并不会违背我们的不变式。

Dynamic Vertex Connectivity

上面我们考虑了边动态变化时的连通性问题，下面我们考虑另一个模型，此时结点动态变化下我们仍然考虑连通性问题。

相关文献为FOCS 2018的文章 ”Dynamic Connectivity: Connecting to Networks and Geometry“。

在这个模型中，给定一张图，每个结点都存在着“开”和“关”两个状态，我们不断更新结点的状态，希望维护连通性问题

如下图所示：

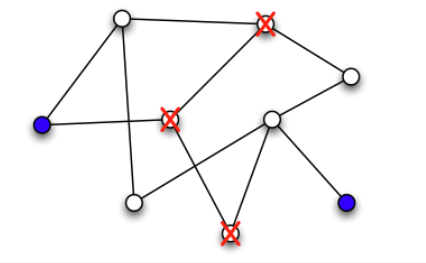
首先我们知道由于每个节点至多连接了 $n$ 条边，因此一个naive的方法是看作边动态变化的连通性问题，但是这样至少需要 $\tilde O(n)$ 的时间，我们希望一个次线性时间的算法。下面我们介绍文章中所给出的数据结构和对应的算法。

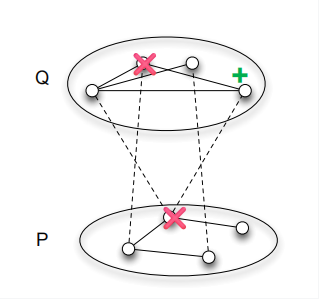
该算法维护一个二部图，如上图所示，结点集合分别为 $P,Q$. 其中集合 $P$ 只支持删除操作，集合 $Q$ 既支持删除又支持添加操作，每次我们把一个结点的状态设置为“开”，都将其放入集合 $Q$ 中。算法每隔一定轮次后就会重新启动，这样可以保证集合 $Q$ 中结点数目被控制住。更具体地，每隔 $m^{2/3}$ 步我们就重新启动，那么集合 $Q$ 的节点数目不超过 $m^{2/3}$. 对于集合 $P$ 中，我们用连通分量进行划分，每个连通分量统一缩成一个结点，我们分为高连通分量和低连通分量，高连通分量的定义为所有结点的度数和超过 $m^{1/3}$ 的连通分量，因此高连通分量的数目不超过 $m^{2/3}$, 如下图所示

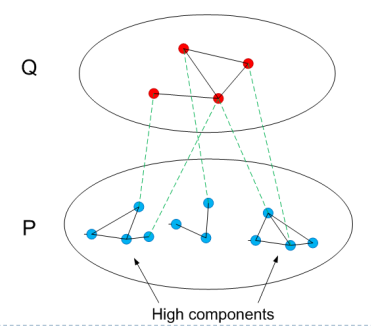
我们希望构造的二部图可以反映原图的连通性，如果 $Q$ 中一个结点和 $P$ 中一个高连通分量中的任意结点有边相连，我们就将这个连通分量和该结点之间连上一条边。但我们还需要考虑低连通分量，由于低连通分量很多，我们不希望也像高连通分量一样处理，我们的做法是：对于 $Q$ 中的两个结点，如果他们都和某一个低连通分量相连，那么我们给这两个结点之间连上一条边，注意到这种方式的两个结点之间可能会存在多重边。这样的边集合我们记作 $\Gamma$, 对于每条连接 $Q$ 中一个结点和 $P$ 中一个低连通分量的一条边，该连通分量至多连接着 $m^{1/3}$ 条边，所以我们知道 $\Gamma$ 的集合大小至多为 $m^{4/3}$.

每次重新启动，我们都需要建立这样大小的一个 $\Gamma$, 因此其预处理的时间复杂度为 $O(m^{4/3})$. 但由于我们只在 $m^{2/3}$ 次迭代后进行预处理，所以预处理的摊还意义下的复杂度为 $O(m^{2/3})$.

像这样这种方式，我们定义了一个图 $G^\ast$, 其结点个数为 $O(m^{2/3})$. 根据我们的连边方式，我们维护 $G^\ast$ 中的连通性信息，等价于维护原图的连通性信息。我们用下图解释：

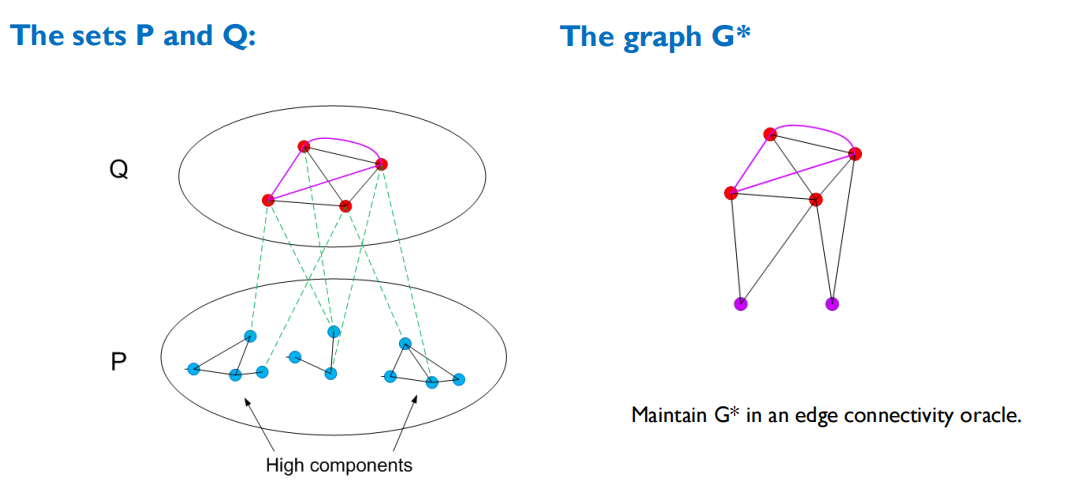
下面我们介绍如何维护这个等价图的连通性信息。

首先我们分析查询时间，对于高连通分量中的结点，我们只需要找到该分量对应相连的 $Q$ 中的结点，然后查询 $Q$ 中的连通性即可。

对于一个低连通分量中的结点，我们可以在 $Q$ 中枚举其所有相邻的边，查看哪一条边对应的结点状态为 “开”，然后我们就可以用 $Q$ 中的该结点表示原来结点。由于低连通分量的度数不超过 $m^{1/3}$, 这个枚举操作的复杂度为 $O(m^{1/3})$. 像这样，对于 $P$ 中的每个结点，如果这个连通分量不孤立，我们都可以将其用 $Q$ 中的某一个结点来表示其连通性，这样转化为 $Q$ 中的连通性，这可以直接进行查询。如果该连通分量是孤立的，我们只要判断另一个结点是否也在这个连通分量内即可，查询也是直接的。因此查询的复杂度不超过 $O(m^{1/3})$.

下面我们分析更新的复杂度。当我们更新集合 $Q$ 中的结点时，我们需要查询这个结点是否和高连通分量或者低连通分量构成一条边。第一类边可以通过枚举所有 $O(m^{2/3})$ 个高连通分量来实现，因此时间复杂度为 $O(m^{2/3})$. 对于第二类边，我们枚举 $Q$ 中的所有点，由于结点数不超过 $O(m^{2/3})$, 总体的时间复杂度也不超过 $O(m^{2/3})$.

下面我们考虑对 $P$ 中的结点的操作，由于 $P$ 只支持删除操作，我们只需要考虑把 $P$ 中的结点状态设置为“关”的情况。我们考虑该结点位于高连通分量还是低连通分量。对于一个低连通分量，我们需要重新计算它所生成的边，由于该连通分量至多只有 $m^{1/3}$ 条边，我们考虑它所连接的 $Q$ 中的两个结点，只需要 $m^{2/3}$ 的复杂度。

对于一个高连通分量，删除结点后整个连通分量可能不在连通，而构成了多个小的连通分量，我们需要对这些连通分量重新连边。如下面的例子所示，下面的左图表示原图，右图表示我们建立的等效图

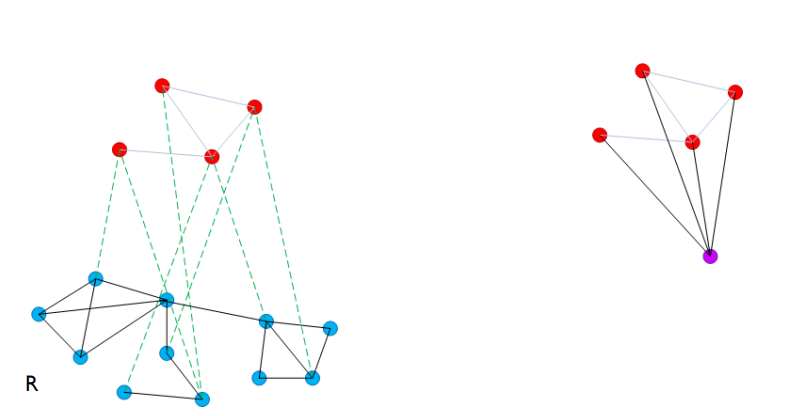
我们考虑删除一个黄色的结点，这样原来蓝色的一整个连通分量分成多个较小的连通分量。

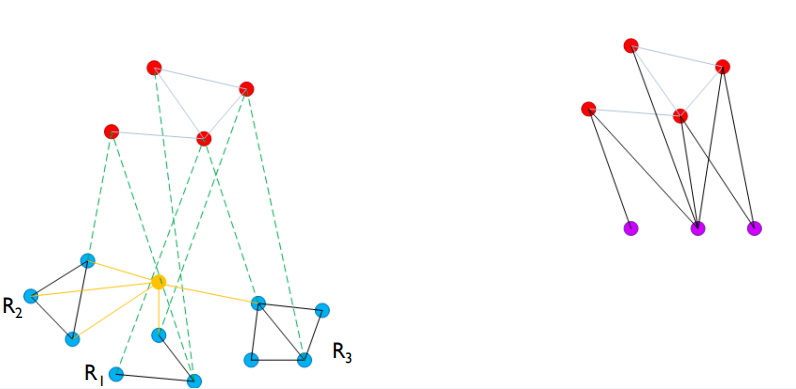
我们将原来连通分量记为 $\gamma$ , 并且用记号 $\gamma_1,\cdots,\gamma_l$ 表示其分成的小连通分量，其中按照连通分量的度数的排序，也就是说， 连通分量 $\gamma_1$ 的度数最高。我们可以将原来的连通分量继承给 $\gamma_1$, 然后其余的连通分量从 $\gamma_1$ 中划分出去，每次划分调用一次cut操作，代价为 $O(\log n)$, 因此整体所有划分的代价为 ${\rm deg}(\gamma_2) + \cdots + {\rm deg}(\gamma_l)$. 上述的每次划分我们都将一条边从原来的连通分量移动到了新的连通分量中，但我们只对较小的连通分量进行该移动操作，每次移动操作至少使得该分量的度数减半，因此一条边总共只可能被移动 $O(\log n)$ 次，因此对于所有的 $m$ 条边，每个阶段中移动的代价也至多为 $\tilde O(m)$, 这被预处理的代价吸收了。

还有一种情况是，在删除高连通分量中的一个结点的时候，产生的新的低连通分量。我们需要计算该新的低连通分量所产生的边集 $\Gamma$.此时需要 $O(m^{2/3})$ 的代价，但我们知道一个阶段中一个结点从高连通分量到低连通分量只能发生一次，而一个阶段中至多只有 $m^{2/3}$ 个操作，因此每个阶段中这部分的代价为 $O(m^{4/3})$, 这同样被预处理的时间吸收掉了。

总体来说，摊还意义下，上述算法更新结点的代价为 $\tilde O(m^{2/3})$, 而查询的时间为 $\tilde O(m^{1/3})$.