近似最短路算法

图上所有结点对最短路的近似算法。

对于一个图，我们令 $n$ 为其结点数，$m$ 为其边数。我们用 $\delta(u,v)$ 表示两个节点之间的最短距离。

注意到对于所有结点最短路问题，Floyd-Warshall 算法可以在 $O(n^3)$ 的时间内解决，本文我们考虑放宽我们的目标，只要求算法输出近似最短路，能否得到更快的算法。

之前关于精确最短路的算法详见 最短路算法.

Additive Approximation

首先我们考虑如下引理，可以通过Chernoff 界证明，此处我们只叙述该引理而略去其证明：

对于任意给定的阈值 $d$, 我们通过随机采样可以得到一个大小为 $\tilde O(n/ d)$ 的结点集合 $D$， 使得图中每个度数大于 $d$ 的结点都与 $D$ 中的一个结点相邻。令 $V_1$ 为度数大于 $n^{1/2}$ 的节点集合，我们通过采样取出集合 $D_1$. 令 $E_2$ 为至少有一个端点不在集合 $V_1$ 中的边的集合。我们考虑如下的算法：我们首先对于所有 $D_1$ 中的结点运行BFS，得到距离 $\delta(D_1 \times V)$, 然后在图 $G’ = (V, E_2 \cup \delta(D_1 \times V))$ 上对于每个结点运行Dijkstra算法 。

我们分析上述算法的复杂度。对 $D_1$ 中的所有结点运行BFS，由于边数 $m = O(n^2)$, 时间为 $\tilde O(n^{5/2})$ . 而图 $G’$ 的边数为 $\tilde O(n^{3/2})$, 因此对所有结点运行Dijkstra算法的时间也为 $\tilde O(n^{5/2})$.

下面分析算法的近似效果。考虑 $u \rightarrow v$ 的最短路径，如果最短路上的所有边的端点的度数都小于 $n^{1/2}$ ，那么最短路径中的所有边都属于集合 $E_2$ , 该最短路径一定可以被找到。我们考虑另外的情况，路径上存在结点其度数大于 $n^{1/2}$, 记最右端的这样子的结点为 $w$, 其与 $V_1$ 中的一个结点 $w’$ 相邻, 如下图所示

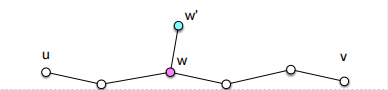
此时我们可以知道算法找到的距离 $d(u,v)$ 一定满足

这说明算法找到了加2意义下的近似最短路。

下面我们进一步给出一个改进的算法，通过增加一层改进算法。我们令 $V_1$ 为度数大于 $n^{2/3}$ 的结点集合， $V_2$ 为度数大于 $n^{1/3}$ 的结点集合。通过采样取大小为 $\tilde O(n^{1/3})$ 的集合 $D_1$， 使得 $V_1$ 中的每个结点至少个$D_1$ 中的某个结点相邻，同理取集合 $D_2$ 大小为 $\tilde O(n^{2/3})$. 类似于上一个算法，我们令 $E_2$ 为存在端点不属于集合 $V_1$ 的边集，大小为 $n^{5/3}$, 同理取边集 $E_3$ 大小为 $\tilde O(n^{4/3})$.

类似于第一个算法，我们先对于 $V_1$ 中所有的结点运行BFS，时间复杂度为 $\tilde O(n^{7/3})$. 然后在从 $D_2$ 的每个结点开始，限制在边集 $E_2$ 上运行BFS， 得到限制在 $E_2$ 上的距离 $\delta’(D_2 \times V)$， 这一步的时间复杂度同样为 $\tilde O(n^{7/3})$. 最后我们定义 $E’ $ 为连接 $V_2$ 中的所有结点到 $D_2$ 中的某个结点的边集，我们知道 $E’$ 的大小为 $\tilde O(n)$. 最终我们对于每个结点 $u$ 在图 $G(V , E_3 \times \delta(D_1 \times V) \times \delta’(D_2 \times {u}) \times E’)$ 中运行Dijkstra算法，复杂度为 $\tilde O(n^{7/3})$. 这里值得注意的是我们并不直接在 图 $G(V , E_3 \times \delta(D_1 \times V) \times \delta’(D_2 \times V))$ 中运行Dijkstra算法, 原因是后面一种做法尽管也可以保证输出一个近似解，但是复杂度不能满足我们的要求。

下面分析算法的输出结果。考虑 $u \rightarrow v$ 的最短路径，如果最短路上的所有边的端点的度数都小于 $n^{1/3}$ ，那么最短路径中的所有边都属于集合 $E_3$ , 该最短路径一定可以被找到. 如果存在一个结点度数大于 $n^{2/3}$, 记最右端的这样子的结点为 $w$, 其与 $ D_1$ 中的一个结点 $w’$ 相邻, 那么根据和上一个算法完全相同的分析，我们知道我们在 $\delta(D_1 \times V)$ 中运行的结果可以找到加2意义下的近似最短路。因此只剩下最后一种情况：最短路径上所有结点的度数都小于 $n^{2/3}$ , 但又存在一个结点度数大于 $n^{1/3}$, 记最右端的这样子的结点为 $w$, 其一定可以通过 $E’$ 中的某条边与 $D_2$ 中的一个结点 $w’$ 相邻，我们作出和之前完全一样的图示：

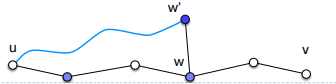
我们知道 $u \rightarrow w$ 中的所有边都包含在 $E_2$ 中，因此在 $\delta’(D_2 \times { u})$ 上运行的最短路算法可以找到 $\delta(u,w)$.

根据我们的定义，我们知道边 $(w,w’)$ 在集合 $E’$ 中，而且 $w \rightarrow w’$ 中的所有边都包含在 $E_3$ 中。

因此我们所给出的距离估计 $d(u,v)$ 满足

这就给出了加2意义下的近似最短路的 $\tilde O(n^{7/3})$ 的算法。

Multiplicative Approximation

上一节考虑的是无权图上加性意义下的近似最短路算法，本节我们考虑带权图（假设权重都为正数），此时加性进行不再具有意义，我们希望寻找乘性意义下的近似最短路算法。我们考虑如下算法：算法中，我们定义 $B(v)$ 为每个结点最近的 $n^{2/3}$ 个结点，同样地利用随机采样我们可以得到集合 $D$ 使得对于每一个结点 $v$ 都存在一个 $D$ 中的元素在 $B(v)$ 中，这样的集合 $D$ 的大小为 $\tilde O(n^{1/3})$. 注意到对每个结点运行使用截断的Dijkstra算法，我们可以在 $\tilde O(n^{7/3})$ 的时间寻找到所有的 $\delta(v \times B(v))$ ，其中比标准Dijkstra的区别在于，每次松驰操作并不考虑一个结点的所有 $n$ 条边，而是仅考虑其权重最小的前 $n^{2/3}$ 条边，由于我们只需要找到 $v$ 到 $B(v)$ 中结点的距离，容易验证上述算法的正确性。最后我们都所有 $D$ 中的结点运行完整的Dijkstra算法，复杂度同样为 $\tilde O(n^{7/3})$.

对于 $u \rightarrow v$ 的最短路，如果 $u$ 或者 $v$ 在集合 $D$ 中，显然第二阶段就已经找到了一条最短路。如果 $v \in B(u)$, 那么第一阶段也找到了一条最短路。只剩下 $v \notin B(u)$ 的情况，我们用下图来形象表明如何得到一个近似解

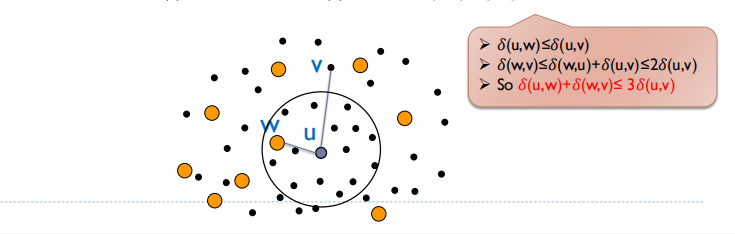
证明其实已经在图中展现，根据 $D$ 的定义我们知道存在 $D$ 中的一个元素 $w$ 满足 $w \in B(u)$, 然后只要输出 $\delta(u,w) + \delta(w,v)$ 根据上图的分析就可以得到乘3意义下的近似最短路。